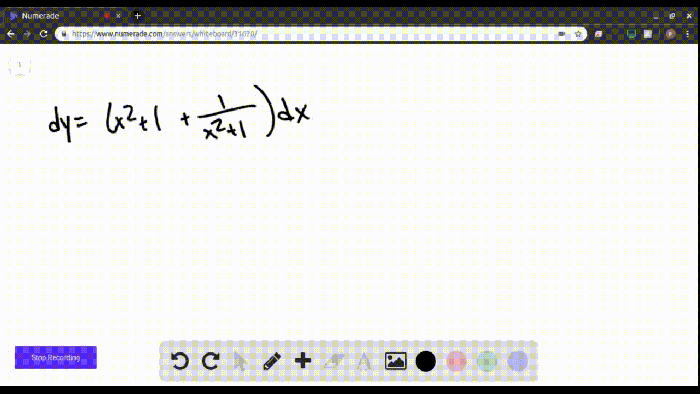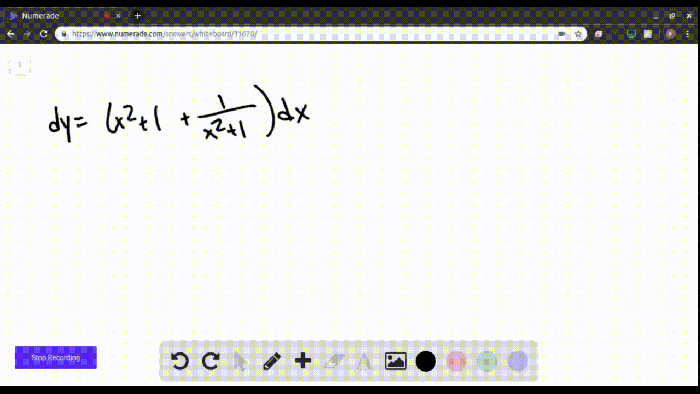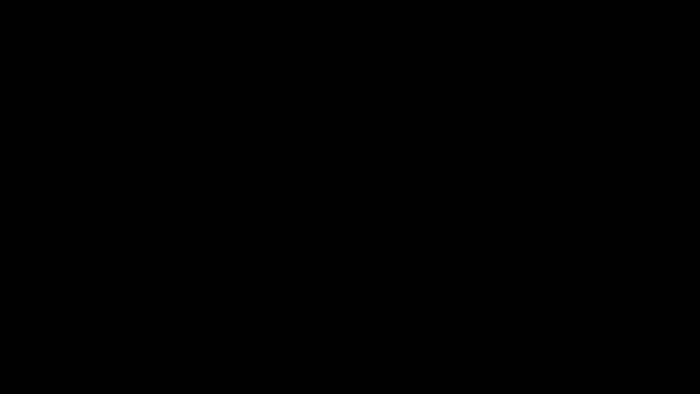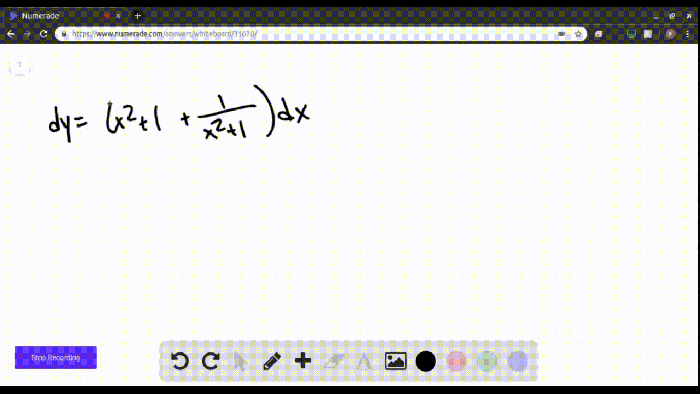
How is rewriting literal equations useful when solving problems? This question delves into the transformative power of manipulating literal equations to simplify complex mathematical expressions, enhance understanding, and uncover hidden relationships. By exploring the benefits, applications, and limitations of rewriting literal equations, we unlock a powerful tool that empowers problem-solvers across diverse fields.

Rewriting literal equations involves expressing a variable in terms of other variables and constants. This strategic transformation allows for the isolation of specific variables, the simplification of complex equations, and the derivation of new insights. The versatility of literal equation rewriting extends to various disciplines, including physics, engineering, economics, and chemistry, where it facilitates the analysis and modeling of real-world phenomena.

1. Understanding Rewriting Literal Equations

Rewriting literal equations involves transforming an equation with a variable on one side into an equation with the variable on the other side. This process allows for the isolation of the variable and the determination of its value.

Methods for Rewriting Literal Equations

• Adding or subtracting the same quantity from both sides:This method is used to isolate the variable on one side by adding or subtracting a constant from both sides of the equation.
• Multiplying or dividing both sides by the same non-zero quantity:This method is used to isolate the variable by multiplying or dividing both sides of the equation by a constant that is not equal to zero.
• Combining like terms:This method is used to simplify the equation by combining terms with the same variable and exponent.

Examples of Rewriting Literal Equations

• Rewrite the equation 2x- 5 = 11 to isolate x:
  • Add 5 to both sides: 2x – 5 + 5 = 11 + 5
  • Simplify: 2x = 16
  • Divide both sides by 2: x = 8
• Rewrite the equation V = lwh to isolate l:
  • Divide both sides by wh: V / wh = l
  • Simplify: l = V / wh

2. Benefits of Rewriting Literal Equations

Rewriting literal equations offers several advantages for problem-solving:

Simplifying Problem-Solving

By isolating the variable, rewriting literal equations simplifies the process of finding its value. This makes it easier to solve complex equations and determine the unknown quantity.

Versatility

Rewriting literal equations can be applied to a wide range of problems, making it a versatile tool for solving equations in different contexts.

Real-World Applications

Rewriting literal equations has practical applications in various fields, such as engineering, physics, and chemistry, where it is used to solve problems involving variables and constants.

Examples of Real-World Applications

• Engineering:Determining the length of a beam based on its cross-sectional area and weight.
• Physics:Calculating the velocity of an object based on its displacement and time.
• Chemistry:Determining the concentration of a solution based on its volume and mass.

3. Applications of Rewriting Literal Equations

Rewriting literal equations finds applications in various fields:

Mathematics

Rewriting literal equations is a fundamental technique in algebra for solving equations and simplifying expressions.

Science

In physics, chemistry, and other sciences, rewriting literal equations is used to derive formulas and solve problems involving variables and constants.

Engineering

Engineers use literal equation rewriting to design and analyze systems, such as calculating the load-bearing capacity of a bridge or the efficiency of an engine.

Economics, How is rewriting literal equations useful when solving problems

Rewriting literal equations is applied in economics to model and analyze economic relationships, such as the relationship between supply and demand.

Case Studies

• Case Study 1:Using literal equation rewriting to design a water distribution system for a city.
• Case Study 2:Applying literal equation rewriting to analyze the performance of a manufacturing process.

4. Limitations of Rewriting Literal Equations

While rewriting literal equations is a powerful technique, it has certain limitations:

Non-Linear Equations

Rewriting literal equations is not applicable to non-linear equations, which cannot be transformed into linear form.

Equations with Multiple Variables

Rewriting literal equations becomes more complex when dealing with equations involving multiple variables, as it may not be possible to isolate each variable.

Equations with Constraints

Rewriting literal equations may not be appropriate for equations with constraints, such as inequalities or equations involving absolute values.

Examples of Problems Not Solvable by Literal Equation Rewriting

• Non-Linear Equation:y = x^2 + 1
• Equation with Multiple Variables:2x + 3y = 6
• Equation with Constraints:|x – 2| > 5

Commonly Asked Questions: How Is Rewriting Literal Equations Useful When Solving Problems

What are the primary benefits of rewriting literal equations?

Rewriting literal equations offers several advantages, including the simplification of complex expressions, the isolation of specific variables, and the derivation of new insights.

In which fields is literal equation rewriting commonly applied?

Literal equation rewriting finds applications in diverse fields such as physics, engineering, economics, and chemistry, where it facilitates the analysis and modeling of real-world phenomena.

Are there any limitations to rewriting literal equations?

While literal equation rewriting is a powerful technique, it may not be appropriate in all situations. For instance, when dealing with nonlinear equations or equations involving multiple variables, alternative approaches may be more suitable.