Special right triangles 30-60-90 worksheet answers are not just a collection of solutions; they are a gateway to understanding the captivating world of geometry. Within these triangles lies a treasure trove of unique properties, ratios, and proportions that have fascinated mathematicians for centuries.

From unraveling architectural enigmas to navigating the complexities of engineering marvels, special right triangles 30-60-90 have proven their indispensable value. Join us as we embark on an enlightening journey, exploring the intricacies of these triangles and their myriad applications.

Special Right Triangles 30-60-90 Basics: Special Right Triangles 30-60-90 Worksheet Answers

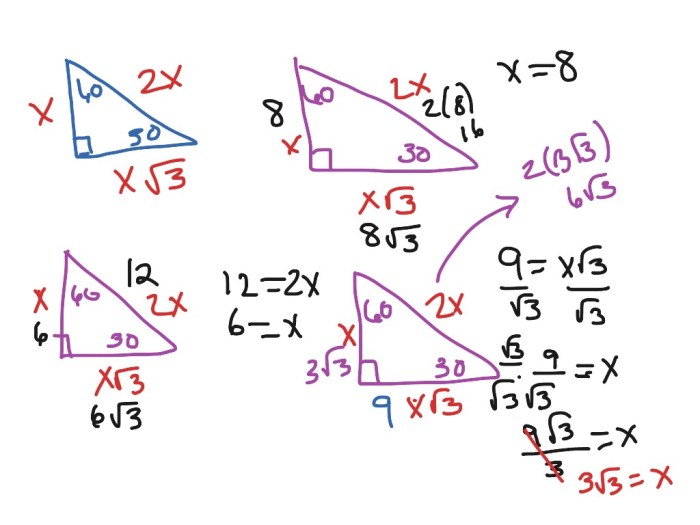
Special right triangles 30-60-90 are unique due to their consistent angle measurements and side length ratios. They are characterized by a 30-degree angle, a 60-degree angle, and a 90-degree angle. Additionally, the side lengths of these triangles are in a specific ratio of 1:√3:2.

Properties of 30-60-90 Triangles

• The shortest side, opposite the 30-degree angle, is denoted as “a”.
• The side adjacent to the 30-degree angle and opposite the 60-degree angle is denoted as “b”.
• The hypotenuse, opposite the 90-degree angle, is denoted as “c”.
• The ratio of the side lengths is: a:b:c = 1:√3:2.
• The area of a 30-60-90 triangle can be calculated as (1/2) – a – b.

Applications of 30-60-90 Triangles

30-60-90 triangles find practical applications in various fields:

• Geometry:Calculating the heights, distances, and angles of objects using the properties of 30-60-90 triangles.
• Architecture:Designing structures and buildings with specific proportions and angles.
• Engineering:Determining forces, moments, and stresses in structures and systems.

Solving Problems with 30-60-90 Triangles

Solving problems using 30-60-90 triangles involves applying the specific ratios and properties:

• Identify the given information:Determine the known side lengths or angles.
• Use the ratios:Apply the ratios of 1:√3:2 to find the unknown side lengths.
• Calculate the area:If necessary, use the formula (1/2) – a – b to find the area of the triangle.

Special Right Triangles 30-60-90 and Trigonometry, Special right triangles 30-60-90 worksheet answers

30-60-90 triangles have a significant relationship with trigonometry:

• Trigonometric functions:The ratios of side lengths in a 30-60-90 triangle are equal to the sine, cosine, and tangent of the 30-degree and 60-degree angles.
• Simplifying calculations:Using 30-60-90 triangles allows for easier calculation of trigonometric functions without using a calculator.

FAQ Insights

What are the unique properties of 30-60-90 triangles?

30-60-90 triangles possess specific ratios between their side lengths: the shortest side is always opposite the 30-degree angle, the longest side is opposite the 90-degree angle, and the remaining side is opposite the 60-degree angle. These ratios give rise to unique proportions and relationships within the triangle.

How are 30-60-90 triangles used in real-world applications?

30-60-90 triangles find applications in various fields, including architecture, engineering, and surveying. They are used to calculate heights, distances, and angles in structures, buildings, and landscapes.

What is the significance of 30-60-90 triangles in trigonometry?

30-60-90 triangles play a crucial role in trigonometry, as they provide a foundation for understanding trigonometric ratios. The ratios of the side lengths correspond to the sine, cosine, and tangent functions, which are essential for solving trigonometric problems.