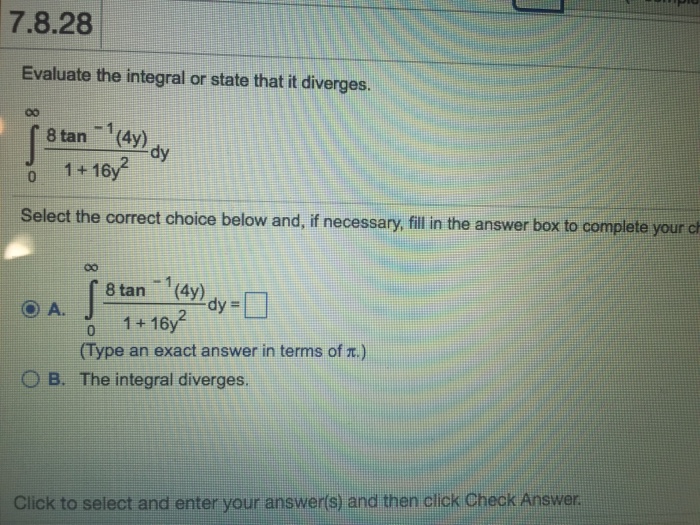
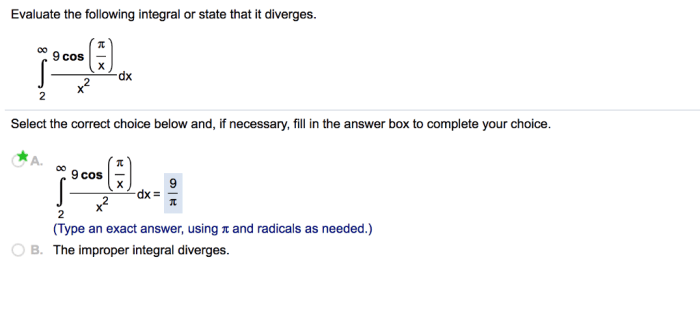
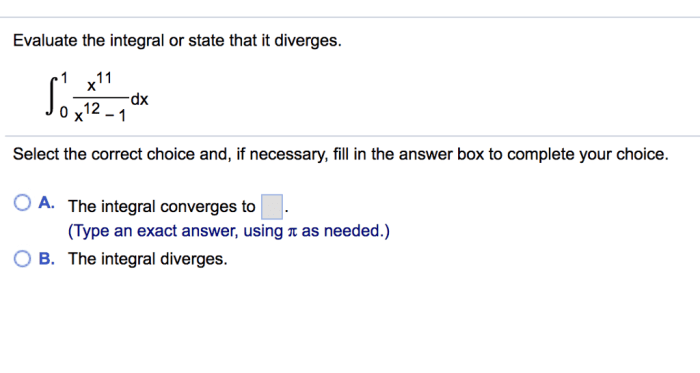
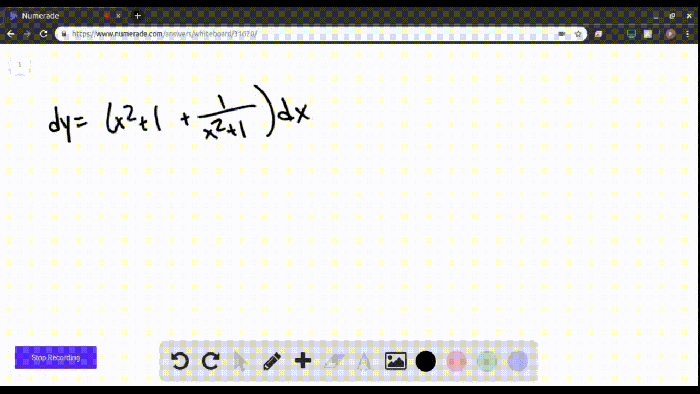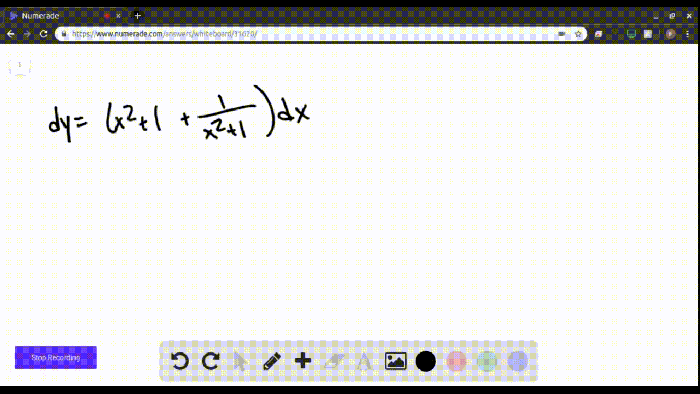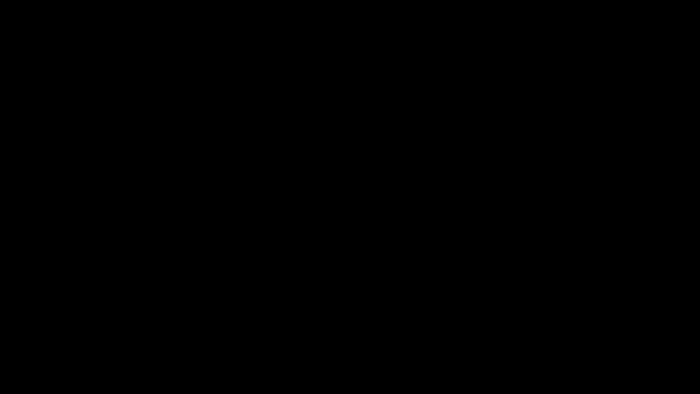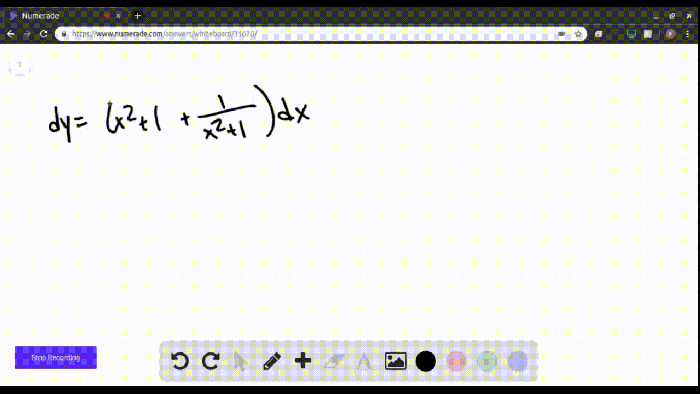
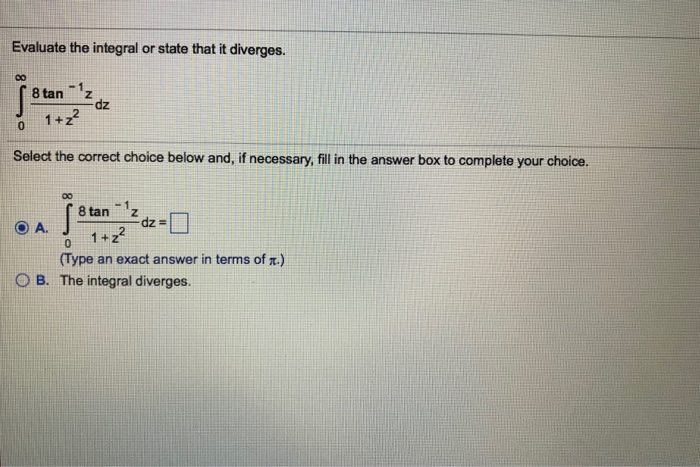
Evaluate the integral or state that it diverges – Evaluating integrals is a fundamental mathematical operation that plays a vital role in calculus. It involves finding the area under a curve, calculating volumes, and solving differential equations. However, not all integrals can be evaluated, and some may diverge, meaning their value approaches infinity or does not exist.
This comprehensive guide will delve into the concept of integral evaluation, exploring the methods used to evaluate integrals, the conditions under which integrals diverge, and the applications of integral evaluation in various fields.
Integral Evaluation
Integral evaluation is the process of finding the value of an integral. Integrals are used to calculate areas, volumes, and other quantities in mathematics and physics. There are a variety of methods for evaluating integrals, each with its own advantages and disadvantages.
Methods of Evaluation
- Substitution: Substitution is a technique for evaluating integrals that involves replacing a variable in the integrand with another variable. This can simplify the integral and make it easier to evaluate.
- Integration by parts: Integration by parts is a technique for evaluating integrals that involves integrating by parts. This can be used to reduce the order of the integral and make it easier to evaluate.
- Partial fractions: Partial fractions is a technique for evaluating integrals that involves decomposing the integrand into a sum of simpler fractions. This can make it easier to integrate the integrand and evaluate the integral.
- Trigonometric identities: Trigonometric identities can be used to evaluate integrals that involve trigonometric functions. These identities can be used to simplify the integrand and make it easier to integrate.
- Numerical integration: Numerical integration is a technique for evaluating integrals that involves using a numerical method to approximate the value of the integral. This can be used to evaluate integrals that cannot be evaluated analytically.
Divergence of Integrals, Evaluate the integral or state that it diverges
An integral is said to diverge if its value is infinite. There are a number of conditions that can cause an integral to diverge, including:
- The integrand is not bounded on the interval of integration.
- The interval of integration is infinite.
- The integrand has a singularity at one or more points on the interval of integration.
Applications of Integral Evaluation
Integral evaluation has a wide range of applications in mathematics, physics, and engineering. Some of the most common applications include:
- Calculating the area of a region
- Calculating the volume of a solid
- Calculating the work done by a force
- Calculating the flux of a vector field
- Solving differential equations
Clarifying Questions: Evaluate The Integral Or State That It Diverges
What is the difference between an integral and a derivative?
An integral is an operation that finds the area under a curve, while a derivative is an operation that finds the slope of a curve.
Why do some integrals diverge?
Integrals diverge when the area under the curve is infinite or does not exist. This can occur when the function being integrated has a vertical asymptote or oscillates infinitely.
What are the applications of integral evaluation?
Integral evaluation has applications in physics, engineering, economics, and other fields. It is used to calculate volumes, forces, work, and many other quantities.