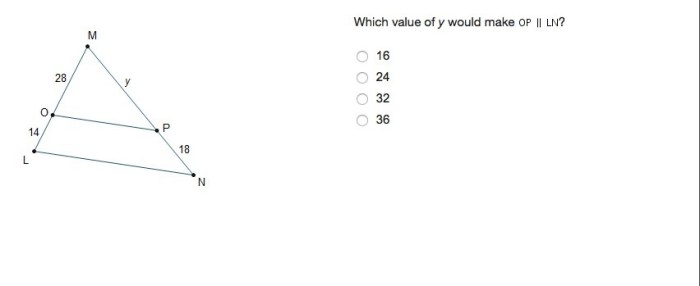
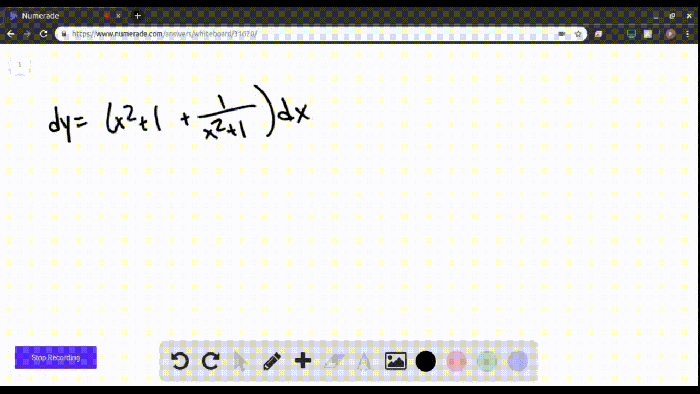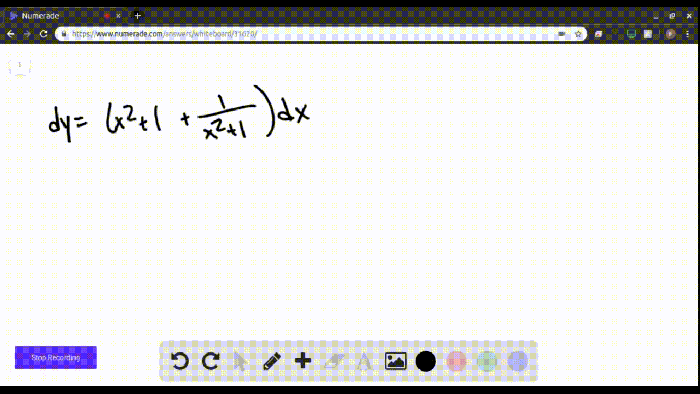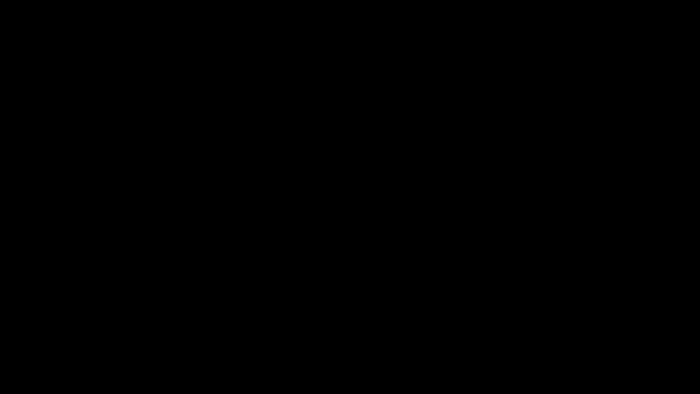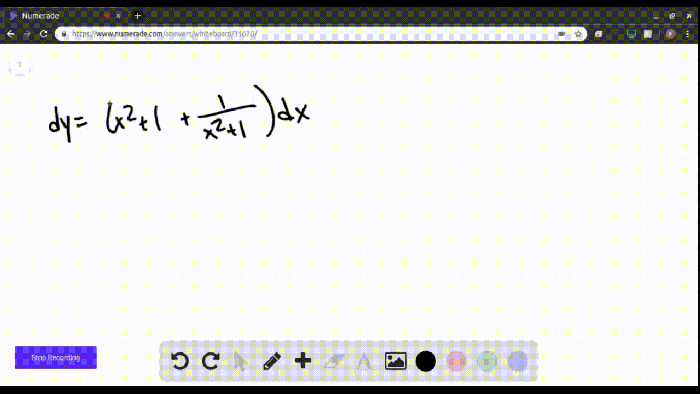
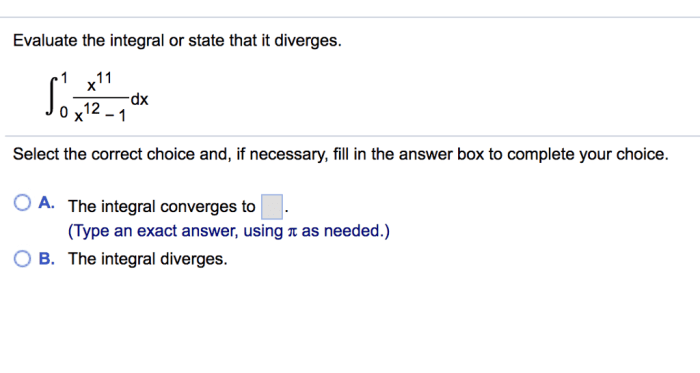
Beginning with which value of y would make op ln, the narrative unfolds in a compelling and distinctive manner, drawing readers into a story that promises to be both engaging and uniquely memorable.
The natural logarithm function (ln) and the exponential function (e^x) are two fundamental mathematical functions that play a crucial role in various scientific and engineering disciplines. Understanding the relationship between these functions is essential for solving equations involving ln and e^x, and for analyzing the value of y that makes op ln.
Natural Logarithm (ln) and Exponential Function (e^x)

The natural logarithm function (ln) and the exponential function (e^x) are two important mathematical functions that are closely related. In this article, we will explore the concepts, properties, and applications of these functions.
The Natural Logarithm Function (ln), Which value of y would make op ln
The natural logarithm function, denoted by ln(x), is the inverse function of the exponential function. It is defined as the power to which the base e (approximately 2.718) must be raised to obtain x. In other words, if ln(x) = y, then e^y = x.
The natural logarithm has several important properties:
- ln(1) = 0
- ln(e) = 1
- ln(xy) = ln(x) + ln(y)
- ln(x^n) = n ln(x)
The Exponential Function (e^x)
The exponential function, denoted by e^x, is the inverse function of the natural logarithm. It is defined as the value of e (approximately 2.718) raised to the power of x. In other words, if e^x = y, then ln(y) = x.
The exponential function has several important properties:
- e^0 = 1
- e^1 = e
- e^(x + y) = e^x – e^y
- e^(cx) = (e^x)^c
Relationship Between ln and e^x
The natural logarithm and the exponential function are inverse functions, meaning that they undo each other’s operations. For example, if you apply ln to e^x, you get x back:
“`ln(e^x) = x“`
Similarly, if you apply e^x to ln(x), you get x back:
“`e^(ln(x)) = x“`
This relationship is useful for solving equations involving ln and e^x.
Solving Equations Involving ln and e^x
Equations involving ln and e^x can be solved using a variety of techniques. Here are a few common methods:
- Using the inverse relationship:If you have an equation involving ln, you can use the inverse relationship to rewrite it in terms of e^x. Similarly, if you have an equation involving e^x, you can use the inverse relationship to rewrite it in terms of ln.
- Using properties of logarithms:The properties of logarithms can be used to simplify equations involving ln. For example, the product rule can be used to combine multiple terms with ln into a single term.
- Using properties of exponentials:The properties of exponentials can be used to simplify equations involving e^x. For example, the power rule can be used to rewrite e^(cx) as (e^x)^c.
Applications of ln and e^x
The natural logarithm and the exponential function have a wide range of applications in various fields, including:
- Mathematics:ln and e^x are used in calculus, probability, and other areas of mathematics.
- Science:ln and e^x are used in physics, chemistry, and other sciences to model exponential growth and decay.
- Finance:ln and e^x are used in finance to model compound interest and other financial concepts.
- Computer science:ln and e^x are used in computer science to model the growth of algorithms and other computational processes.
FAQ Explained: Which Value Of Y Would Make Op Ln
What is the natural logarithm function?
The natural logarithm function, denoted as ln(x), is the inverse of the exponential function e^x. It is defined as the power to which e must be raised to obtain x.
What is the relationship between ln and e^x?
ln and e^x are inverse functions, meaning that ln(e^x) = x and e^(ln(x)) = x. This relationship allows us to solve equations involving both functions.
How do I find the value of y that makes op ln?
To find the value of y that makes op ln, we need to solve the equation op = ln(y) for y. This can be done using algebraic techniques or by using a calculator.